
|
| |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
 |
|
The problem by Lavrentyev and Ishlinsky. Elaboration of the idea
The foundations of investigations on the static stability of rods were laid in works by Euler in 1744. Experimental and theoretical investigations indicate the necessity of rather careful application of static methods in conditions of dynamic loading. Lavrentyev and Ishlinskii in classic paper [M. A. Lavrent’ev and A. Yu. Ishlinsky, Dokl. Akad. Nauk 64 (6), 776 (1949).] paid attention to the specifics of the results found when investigating the stability of the rod under the effect of shock loading. It is established that with intense loading, which essentially exceeds the Euler static critical load, the largest rise rate of the amplitude is inherent to the form with a large number of waves in the longitudinal direction.
The influence of propagation of longitudinal waves over the rod length was investigated in subsequent studies for various statements. The possibility of the appearance of parametric resonances leads particularly to the loss of stability at loads smaller than the Euler load. With the short-term shock in the linear statement, the parametric resonance leads to an infinite amplitude rise. In the quasi-linear statement, at which the longitudinal deformation is calculated by the nonlinear formula
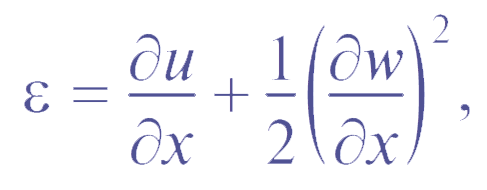
with the parametric resonance, the beat mode with the energy transfer of transverse vibrations into longitudinal ones and vice versa is implemented.
|


|
XI Всероссийский Съезд по Фундаментальным Проблемам Теоретической и Прикладной Механики Казань, 19-24 августа 2015г.
1. Belyaev A.K., Morozov N.F., Tovstik P.E., Tovstik T.P. The problem by Lavrentyev and Ishlinsky. Elaboration of the idea. Presentation (in Russian). (4.9 Mb) Abstract (in Russian).(1.6 Mb)
2. Morozov N.F., Tovstik P.E. The rod dynamics under longitudinal impact. Book of Abstr. Int. Conf. on Nonlinear Dynamics in Engineering: Modeling, Analysis and Applications. 2013. P.73. Aberdeen. UK. (72 Kb)
3. Morozov N.F., Tovstik P.E. Doklady Physics. Transverse rod vibrations under a short-term longitudinal impact. Doklady Physics. September 2013, Volume 58, Issue 9, pp 387-391.
4. Morozov N.F., Tovstik P.E. Doklady Physics. Dynamic Loss of Stability of a Rod under Longitudinal Load Lower than the Eulerian Load. Doklady Physics. November 2013, Volume 58, Issue 11, pp 510-513.
5. Morozov N.F., Tovstik P.E., Tovstik T.P. Doklady Physics. Again on the Ishlinskii–Lavrentyev Problem. Doklady Physics. April 2014, Volume 59, Issue 4, pp 189-192.
6. Morozov N.F., Belyaev A.K., Tovstik P.E., Tovstik T.P. The Ishlinsky-Lavrentiev problem at the initial stage of motion. Doklady Physics. 2015.
7. Belyaev A.K., Morozov N.F., Tovstik P.E., Tovstik T.P. Dynamic behavior of a thin elastic rod under the longterm longitudinal compression. 5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2015). (1.32 Mb)
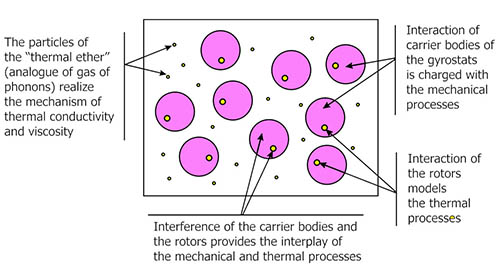
For modeling a material medium we use the one-rotor gyrostat continuum. It is shown that the mathematical description of this model in special cases is reduced to the equations of the coupled thermoelasticity problem, to the equation of self-diffusion, and also to the equation, which describes the flow of the viscous incompressible fluid.
Within the framework this model is given original treatment of the mechanism of thermal conductivity and internal friction. Keywords: thermal conductivity, internal damping.
Ivanova E.A. "The new equations of thermoviscoelasticity". Scientific report 21.03.2011г IPME RAS. (In Russian) (454 Kb)
1. Ivanova E.A., Krivtsov A.M., Zhilin P.A. Description of rotational molecular spectra by means of an approach based on rational mechanics. ZAMM. Z. Angew. Math. Mech. 87 (2007) N 2. P. 139-149. (135 Kb)
2. Ivanova E.A. On one approach to formulation of the coupled problem of thermoelasticity with the hyperbolic type heat conduction equation. Fifth Polykhov's reading. Selected Works of Int. Conf. on Mechanics. St. Petersburg. 2009. P. 301-306. (In Russian) (376 Kb)
3. Ivanova E.A. Derivation of theory of thermoviscoelasticity by means of two-component medium. Acta Mechanica. 2010. Vol. 61, Issue 1. P. 261-286. (184 Kb)
4. Ivanova E.A. On one model of generalised continuum and its thermodynamical interpretation. Mechanics of generalized Continua (Ed. H. Altenbach, G.A. Maugin, V. Erofeev). Berlin: Springer, 2011. P. 151-174. (400 Kb)
5. Ivanova E.A. Derivation of theory of thermoviscoelasticity by means of two-component Cosserat continuum. Technische Mechanik. 2012. Vol. 32, Issue 2-5. P. 273-286. (128 Kb)
6. Ivanova E.A. Modeling of thermoelastic processes in three-dimensional media and shells by means of the Cosserat continuum with micristructure. Radio electronics. Nanosystems. Information technology. 2013. Vol. 5. N 1. P. 98-110. (In Russian) (1374 Kb)
7. Babenkov M.B., Ivanova E.A. Analysis of the wave propagation processes in heat transfer problems of the hyperbolic type. Continuum Mech. Thermodyn. Published on-line: 11 August 2013. DOI 10.1007/s00161-013-0315-8. (824 Kb)
8. Ivanova E.A. Description of mechanism of thermal conduction and internal damping by means of two component Cosserat continuum. Acta Mechanica. Published on-line: 27 September 2013. DOI 10.1007/s00707-013-0934-y. (280 Kb)
We consider the density of the number of particles and the density of mass as the independent variables and we consider internal energy and entropy the additive functions of the number of particles. Our approach allows us to describe both phase states with different mechanical and thermodynamic parameters in a framework of a unified model. At the same time our approach allows us to describe the behavior of matter immediately during the phase transition. Keywords: Phase transitions.
1. Vilchevskaya E.N., Ivanova E.A., Altenbach H. Description of liquid-gas phase transition in the frame of continuum mechanics. // Continuum Mech. Thermodyn. Published on-line: 23 April 2013. DOI 10.1007/s00161-013-0298-5. (572 Kb)
2. Vilchevskaya E.N., Ivanova E.A. The reduced equation of energy balance — an alternative approach. Appendix to the book: Zhilin P.A. Rational Continuum Mechanics. St. Petersburg.: Publishing House of the Polytechnic. University Press, 2012. 584 p. (P. 476-485) (In Russian) (192 Kb)
3. Ivanova E.A. Zhilin's method and Truesdell's method — a comparative analysis. Appendix to the book: Zhilin P.A. Rational Continuum Mechanics. St. Petersburg.: Publishing House of the Polytechnic. University Press, 2012. 584 p. (P. 486-495) (In Russian) (196 Kb)
4. Ivanova E.A., Vilchevskaya E.N. Description of thermal and micro-structural processes in generalized continua: Zhilin's method and its modifications. // Generalized Continua as Models for Materials with Multi-scale Effects or Under Multi-field Actions (Ed. H. Altenbach, S. Forest, A.M. Krivtsov). Berlin: Springer, 2013. P. 179-197. (268 Kb)
We consider the microstructure of piezoelectric materials and use the equations of micro-polar continuum by the method suggested by P.A.Zhilin. We propose two theories of piezoelectricity, based on the equations of micro-polar continuum. The first theory describes piezoelectric effect in the polar materials. The second theory describes piezoelectric effect in the non-polar materials. Keywords: polar and non-polar piezoelectrics.
1. Ivanova E.A., Kolpakov Ya.E. The Cosserat continuum and piezoelectricity. Appendix to the book: Zhilin P.A. Rational Continuum Mechanics. St. Petersburg.: Publishing House of the Polytechnic. University Press, 2012. 584 p. (P. 506-531) (In Russian) (284 Kb)
2. Ivanova E.A., Kolpakov Ya.E. The use of moment theory to describe the piezoelectric effect in polar and non-polar materials. Generalized Continua as Models for Materials with Multi-scale Effects or Under Multi-field Actions (Ed. H. Altenbach, S. Forest, A.M. Krivtsov). 2013. Berlin: Springer. P. 163-178. (276 Kb)
3. Ivanova E.A., Kolpakov Ya.E. Description of the piezoelectric effect in polar materials by means of the moment theory. Prikladnaya mekhanika itekhnicheskaya fizika. 2013. Vol. 54. N 6. 15 p. (In Russian)
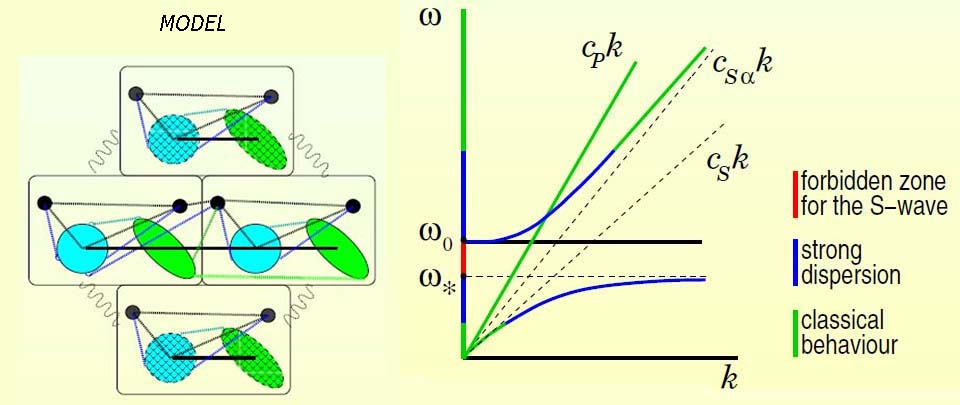
Acoustic metamaterials became popular in recent years. For example, it is possible to use them for a decrease in vibration level, for the monitoring of acoustic waves beam and, possibly, for the extraction of energy.
Is proposed the method of constructing acoustic metamaterials with the forbidden bands of frequencies and the resonance properties. Materials with the forbidden bands of frequencies are constructed by the continuum of complex body-points. Examples: Cosserat reduced medium , birotative medium.
Elena F. Grekova "As to theoretically design acoustic metamaterial with the forbidden bands". Scientific report 20.02.2014 IPME RAS. (In Russian) (405 Kb)
«The motion of the celt attracts researchers’ attention by unusual properties. If we put the celt on a horizontal surface and twist it about its vertical axis, then, after a certain time, it stops rotating about this axis, but vibrations about the other axes may arise and then the celt begins rotating about the vertical axis in the opposite direction". (V. Ph. Zhuravlev, D. M. Klimov, Mechanics of Solids. June 2008, Volume 43, Issue 3, pp 320-327)
The Celt stone dynamics is the classical problem of the nonlinear non-holonomic dynamics of the rigid body. This is classical academical training task. On it worked such well-known scientists as Karapetyan A.V., Markeev A.P., and into the latter several years, academicians Zhuravlev V. Ph., Klimov D.M.
The convex body moves near its stable position of equilibrium on the rough horizontal plane under the action of gravitational force. The complete nonlinear system of equations, which describes the motion of body in the case of the arbitrary tensor of inertia, is obtained. The motion of the Celt stone in the form of ellipsoid and paraboloid are investigate. We analytically found the possible regimes of oscillation, known from experimental studies of other authors. The influence of the body surface form and its tensor of inertia on the possible global motion was investigated.
1. Is carried out a study in the nonclassical setting for the dynamically unbalanced body with the unbalanced of common form.
2. Is analytically obtained the system, which describes the evolution of the amplitudes of main of fluctuations and angular velocity around the vertical axis. It is differed from obtained in the works of Markeev A.P. by including of the larger number of parameters.
3. During investigations of Markeev A.P. and Pascal M. we receive the equation, which describes the motion of body in the averaged setting, into which entered only one parameter equal to the relationship of the natural frequencies squares of the two main vibrations.
4. Are solved problem about the motion with sliding and twisting, proposed by Acad. Zhuravlev V.Ph. We investigate the influence of the size of sliding friction coefficient on the possibility of the appearance “Celt effect” and on the period of the evolution of rotations. Keywords: Celt stone.
1. Tovstik T.P. The Celt rattleback dynamics with the friction influence. // Fourth Polykhov's reading. Selected Works of Int. Conf. on Mechanics. St. Petersburg. 2006. (432 Kb)
2. Tovstik T.P. Analytical and Numerical Research of the Celt Stone Dynamics. // Proceedings of the Second International Conference on Dynamics Vibration and Control. Beijing, China. ICDVC 2006-W47. (127 Kb)
3. Tovstik T.P. On the influence of sliding on the Celt rattleback motion. // Proceedings of XXXV International Summer School-Conference APM-2007, St.Peterburg (Repino), Russia, pp. 432-437. (148 Kb)
The possibilities of mechanics in questions of the description of microcosm are far from exhausted and they are not investigated.
The problem of description at the mechanical level of graphite crystal lattice is solved by use the paired interatomic moment potential of interaction. To the central interaction of two atoms moment component of potential, connected with the orientation of atoms, is added. Two-dimensional and three-dimensional problems are solved.
Statics and dynamics, deformation, stability, fluctuations, propagation of waves are investigated. Keywords: graphite lattice, pairwise interaction, stability, longitudinal and shear waves, acoustic and optical modes.
1. Tovstik T.P. Elastic and dynamical properties of the graphite crystal lattice model. // Proceedings of the Fourth European Conference on Structural Control, St.Petersburg, Russia. 2008. pp. 811-818. (270 Kb)
2. Tovstik T.P. The construction of stable model of the nanotubes and fulleren. // Fifth Polykhov's reading. Selected Works of Int. Conf. on Mechanics. St. Petersburg. 2009. P. 333-338. (In Russian) (270 Kb)
3. Tovstik P.E., Tovstik T.P On the 2D graphite layer model. Vestnik St.Petersburg University. Ser. 1. 2009. Issue 3. P. 134–143. (In Russian)(311 Kb)
4. Tovstik P.E., Tovstik T.P Static and dynamic analysis of two-dimensional graphite lattices. MTT, 2012, №5, P. 35-43. (In Russian) (341 Kb) Mechanics of Solids, September 2012, Volume 47, Issue 5, pp 517-524.
5. Morozov N.F., Tovstik P.E., Tovstik T.P. Continual Model of Deformation of Graphene. // Vestnik S.Peterb. Univ. Math. 2014. 47(1), P. 47-55. (215 Kb)
Works are dedicated to the application of asymptotic methods to the construction of the two-dimensional models of plates and shells and to the analysis of the asymptotic correctness of the classical two-dimensional models of Kirchhoff-Love and Timoshenko-Reissner. This problem leas in the focus of the attention of the mechanics of solids already during more than 150 years; however, the intensity of studies does not decrease in connection with the appearance of new materials and constructions.
Two-dimensional models for the isotropic and orthotropic materials are studied sufficiently fully; however, the general case of the anisotropy, described by 21 elastic module, requires further studies. The problems of statics, fluctuations and stability are solved for the models introduced into the examination. Keywords: plate, shell, anisotropy, asymptotic behavior.
1. Tovstik P.E., Tovstik T.P. On the 2D models of plates and shells including the transversal shear. // ZAMM, 2007, 87, №2, pp. 160-171. (127 Kb)
2. Tovstik P.E., Tovstik T.P. Two-dimensional Models of Plates Made of an Anisotropic Material. // Proceedings of XXXVIII International Summer School-Conference APM-2010, St.Peterburg (Repino), Russia, pp. 733-740. (156 Kb)
3. Tovstik P.E., Tovstik T.P. Buckling problems of a cylindrical shell made of anisotropic material. Vestnik St.Petersburg University. Ser. 1. 2013. Issue 2. (In Russian) (1240 Kb)
4. Tovstik P.E., Tovstik T.P. Two-dimensional models of shells made of an anisotropic material. // Acta mechanica. 2013. September. DOI 10.1007/s00707-013-0926-z.